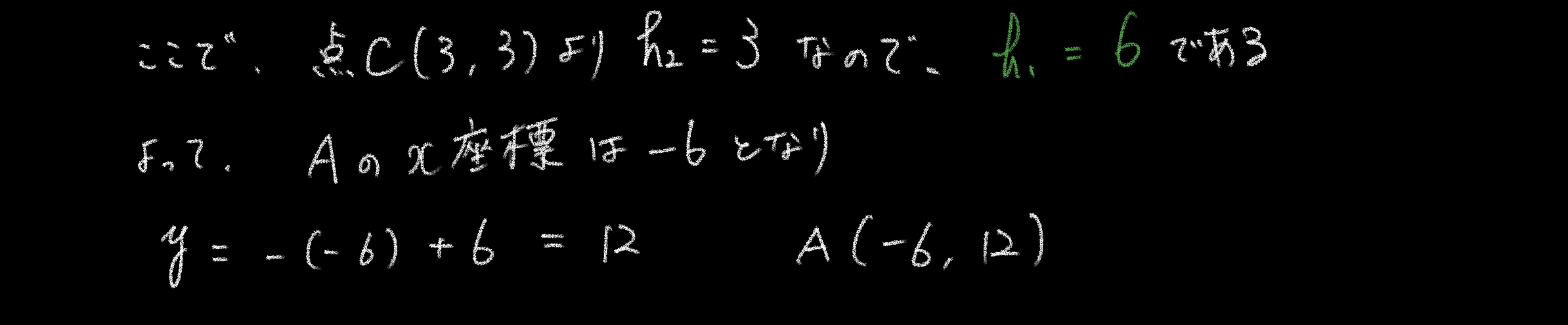2022年度　長野県高校入試 数学の解説

2022年 長野県高校入試 数学 大問3 Ⅱ ②

今回は、2022年度の長野県高校入試から数学の複雑な問題を解説していきます。
実際のテストでこのレベルを解き切るには、普段から解ける問題のパターンを増やし、解き方の手順を自分もものにすることが重要です。
関数の問題は高校生になっても、ひたすら学び続けるため、中学生の時にきちんと概念を理解しておきましょう。
その際は、必ず新研究などの参考書を単元ごと学び直す事がオススメです。出来ると高をくくるコト無く、整理することが基礎の穴埋めにおいて重要です。

大問３ Ⅱ(3) ② 問題

難易度の高そうな問題は逆順で考えていく

問題を見た時に、サクッと解法が浮かばないケースがありますよね。
その場合は、焦らずに問題文で求められている答えから、必要事項を辿っていきましょう。

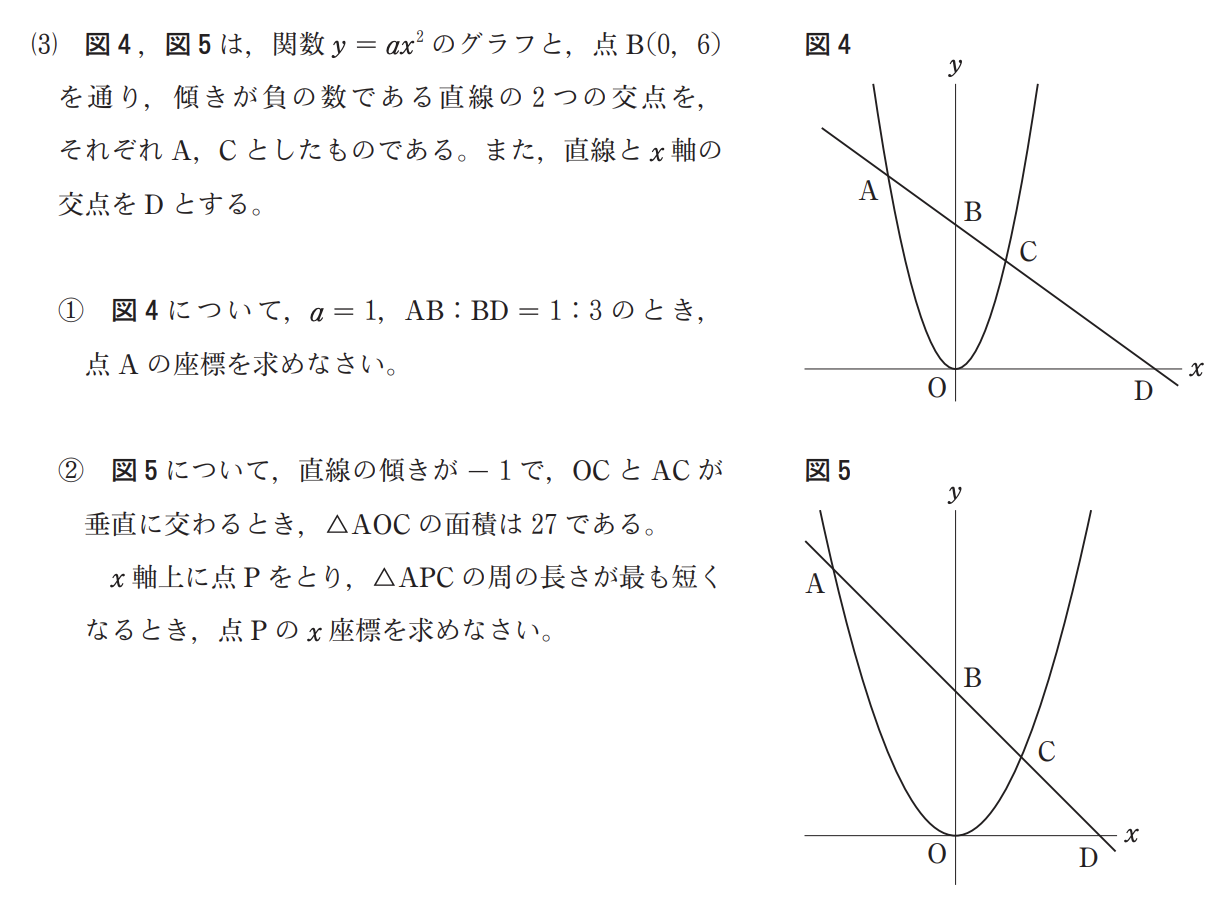
今回は下の解説1にあるように、$\triangle{APC}$の周の長さが最も短くなるときの$点Pのx座標$を求めます。
では、周の長さが最も短くなるとはどんなときでしょうか。
$辺AC$の長さは固定されているので、$点P$の位置によって、$辺AP＋辺PC$の長さが変動すると考えられますね。
しかし、$辺AP＋辺PC$では、$点P$がどこにあれば、最短なのか分かりません。

そこで、作図の問題を思い出しましょう。折り返した直線の最短距離を求める問題を中学1年生で習うはずです。
解説にあるとおり、$点Cとx軸$について対称となる$点C'$を取ります。
すると、図から分かる通り$AP+PC = AP+PC'$という関係になることがわかります。

後は、直感的にも分かる通り、$AP＋PC'$が曲がること無く、直線になる場合が最短であると言えます。

大問３ Ⅱ(3) ② 解説1

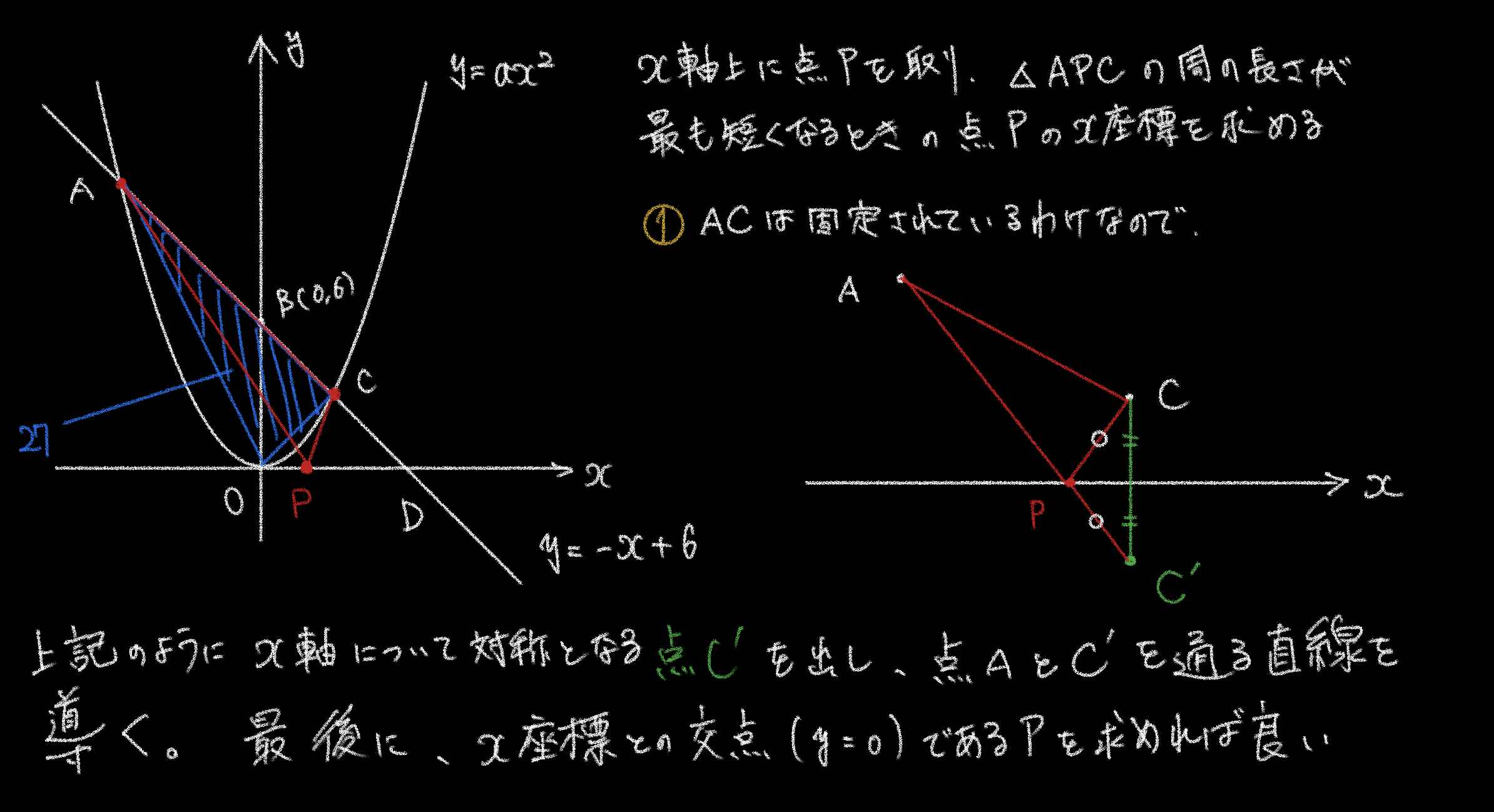
解説１で説明したとおり、必要なのは$点C$の座標です。
これは以下の解説画像のとおり、$\triangle{OBD}$について着目すると$OC$が$AC$と垂直に交わるということから、求めることが出来ます。（$\triangle{OBD}$は直角二等辺三角形）

大問３ Ⅱ(3) ② 解説2

$点C$が判明したら、直線を作るために必要な点Aの座標を求める。
求め方は$\triangle{AOC}=\triangle{AOB}+\triangle{OCB}$を使う。
底辺を共通の$辺OB=6$とし、各高さを$h_{1}, h_{2}$と置き、$\triangle{AOB}+\triangle{OCB} = 27$に代入する。（$点C$が判明しているため、$\triangle{OCB}$の高さを3としても良い。分かりやすさのため、ここでは後から代入している）

大問３ Ⅱ(3) ② 解説3

大問３ Ⅱ(3) ② 解説4

以上で、$点Aと点C$を求められたので、当初の①で言ったとおり、$点Aと点C'$を通る直線$y=ax+b$を求める。
最後に、その直線に$y=0$を代入し、$x軸$との$交点Pのx座標$を出して終了です。

大問３ Ⅱ(3) ② 解説5

当会では、長野県の高校入試を見据えて、小中学生を英数メインで指導しております。（高校生も英検準一級まで、および数学と物理を指導します）
ご興味がある方は、お問い合わせ下さい。