2025年度大学入学共通テストの情報のサンプル問題を解きました

情報科目の調査

私は情報系の学生ではあったものの、大学生から専攻していました。
塾生として指導した学生もプログラミングに関しては、C 言語や JavaScript だったこともあり、普通科の高校生の「情報」科目に対する学習範囲にはまだ浅い所がございます。

そこで、現在の高校一年生の「情報」という科目では、いったいどんな内容を扱い、どんな問題が出るのかを調査しました。

今後は、普通科の高校で与えられる情報の教科書も調達し、より適切な範囲の中で指導が出来るようにしていこうと思います。

大学入試センターの情報のサンプル問題

それでは本題ですが、令和 7 年度の大学入学共通テストでは情報科目が追加されます。
具体的なイメージを共有するため、独立行政法人大学入試センターの Web サイトにて、新しい学習指導要領に対応したサンプル問題（pdf）が公開されています。

>> 令和７年度以降の試験に向けた検討について｜大学入試センター

詳しくは、pdf に作成の趣旨が掲載されておりますので、各人でご確認ください。

第 1 問

問１から問４まであります。各問で、異なる分野の知識が問われています。
当然、対策なしでは解けないような問題も見られました。
問１、問２は一般的な普通科の生徒でも十分に解けるレベルの知識問題だと思います。
問３、４にかけて、情報科学に傾倒した知識が多少必要だと思われます。

問１ 日常的な IT 系サービスの基盤について（日常的に利用するサービスに関する知識）

実際の東日本大震災の後にまとめられた文書を用いた会話文を元に、問題が作成されていました。
「当時、音声通話やメール等が繋がりにくくなったのに対し、SNS を用いたリアルタイムの情報発信、収集が個人、公共機関問わず有効にはたらいた」
という旨の文章に下線 a。
それについて、固定電話の回線交換方式とデータ通信であるインターネット回線によるパケット交換方式の違いで SNS が災害に強かった事を説明する問題でした。以下の画像は、解答に必要となる「固定電話の回線交換方式」と「データ通信であるインターネット回線によるパケット交換方式」の違いに関する解説です。

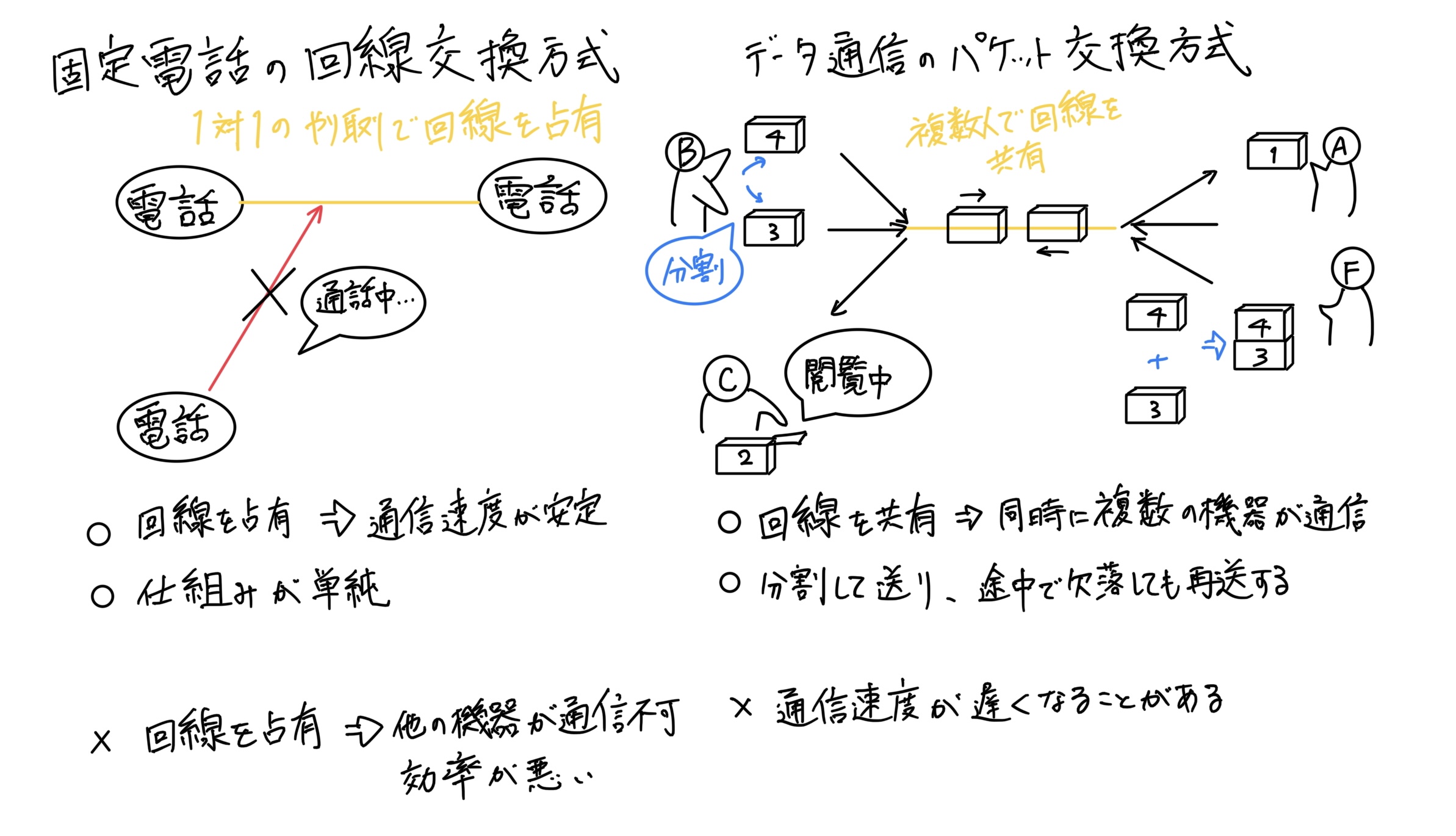
よって、解答ア、イとしては、

• データを送るためのパケットが途中で欠落しても再送
• 回線を占有しないで送信元や宛先の異なるパケットを混在させて送出

となります。
下線部 c に関する解答ウは、情報格差は世代、経済的な違いから生じるということでいいでしょう。災害時に大量に出回った情報は、機密性には関係ないでしょう。また信憑性は格差を生む前に正しい情報も偽の情報も伝達していることになるため、個々人の真偽の目に委ねられるはずです。

続いて、下線 b として「被災した自治体等に対し、HP、メールサービスの提供や避難所の運営支援ツールをクラウド上で提供することも行われた」とあります。こちらはクラウドサービスに関する知識が必要です。

IT 系の開発に関わる知識というよりは、Gmail などのクラウドサービスを既存のダウンロードして使うソフトなどと比較している印象です。クラウド上という言葉の通り、ネットワークを介して、手元のスマホや PC から別の場所にアクセスしてデータをやり取りする仕組みの事です。

自社が用意する自前のサーバー（ウェブサイトやサービスのデータを置き、管理、配信する PC）を使わず、サービス提供会社からネットワークを介し、借り受けるという、例えば Amazon Web Services（AWS）などが有名です。

個々人で利用しているサービスだと Gmail、特にネットワークを介しているという点で今までインストールしていた Microsoft の Word や PowerPoint に対する、Google ドキュメントや Google スライドと言えば分かりやすいかもしれません。

手元にはデータが無くとも、アクセスすればサービスを利用出来ます。よって、解答エは「サーバなどの危機を自ら設置する必要が無い。」ですね。

問２ 資料作成（知識ではなく、正しく内容を表現する手法を選ぶ問題）

ここは、画像だけご覧ください。解説は割愛します。

問３ アナログからデジタルへの変換(情報科学に関する知識が必要)

コンピュータで処理できるように、モノクロの画像の濃淡（連続量）を整数に近似して表現する手法について考えます。

解答クは、「区画の濃淡を一定の規則に従って整数値に置き換えており」となります。これは与えられた図１を見れば解けますね。

解答ケは、知識問題です。このような、自然界の連続的に変化する信号を離散的な値（バラバラの整数値など）に近似して表現する事で、コンピュータで処理出来るようにする事を「量子化」と呼びます。

例えば、今回のケースであれば、濃淡という濃さがグラデーションで（連続的に）変化しているものを、画素と呼ばれる区画で分割し、各区画に整数値で近似します。（近づけて妥協しているだけで、明確にその値というわけではない）

本来であれば、決まった区切りがない代物を区画ごとに整数値を持たせた事で、コンピュータに保存させることが出来ます。一度デジタルデータとして保存された画像などは、複製したり伝送しても、同じ区画に同じ値が存在しており、別のコンピュータでも同じように再現できます。
よって、解答コは「コピーを繰り返したり、伝送したりしても画質が劣化しない。」ですね。

問４ ネットワーク、IP アドレスに関する解説（正しく理解する時間が必要）

IP アドレスについての知識が必要です。私が高校生の頃は、恥ずかしながら全く知らない情報でした。

プライベート IP アドレスとグローバル IP アドレスが存在しますが、グローバル IP アドレスは家の WiFi ルーター（これもネットワーク機器の一つ）などに、契約したプロバイダーから割り振られています。WiFi ルーターから接続している個々のスマホや PC にはプライベート IP アドレスが割り振られています。

また、IP アドレスにもバージョンがあり、有名なのは「IPv4」と「IPv6」ですね。一般的に使われてきたのが「IPv4」で、爆発的にネットワーク機器が増えたことで（インターネット需要の増大）、割り振るアドレスが枯渇してきてしまいました。そこで新しくより複雑で多い組み合わせの番号を利用するルールを決めた事で、使えるアドレスを増やしたものが「IPv6」です。

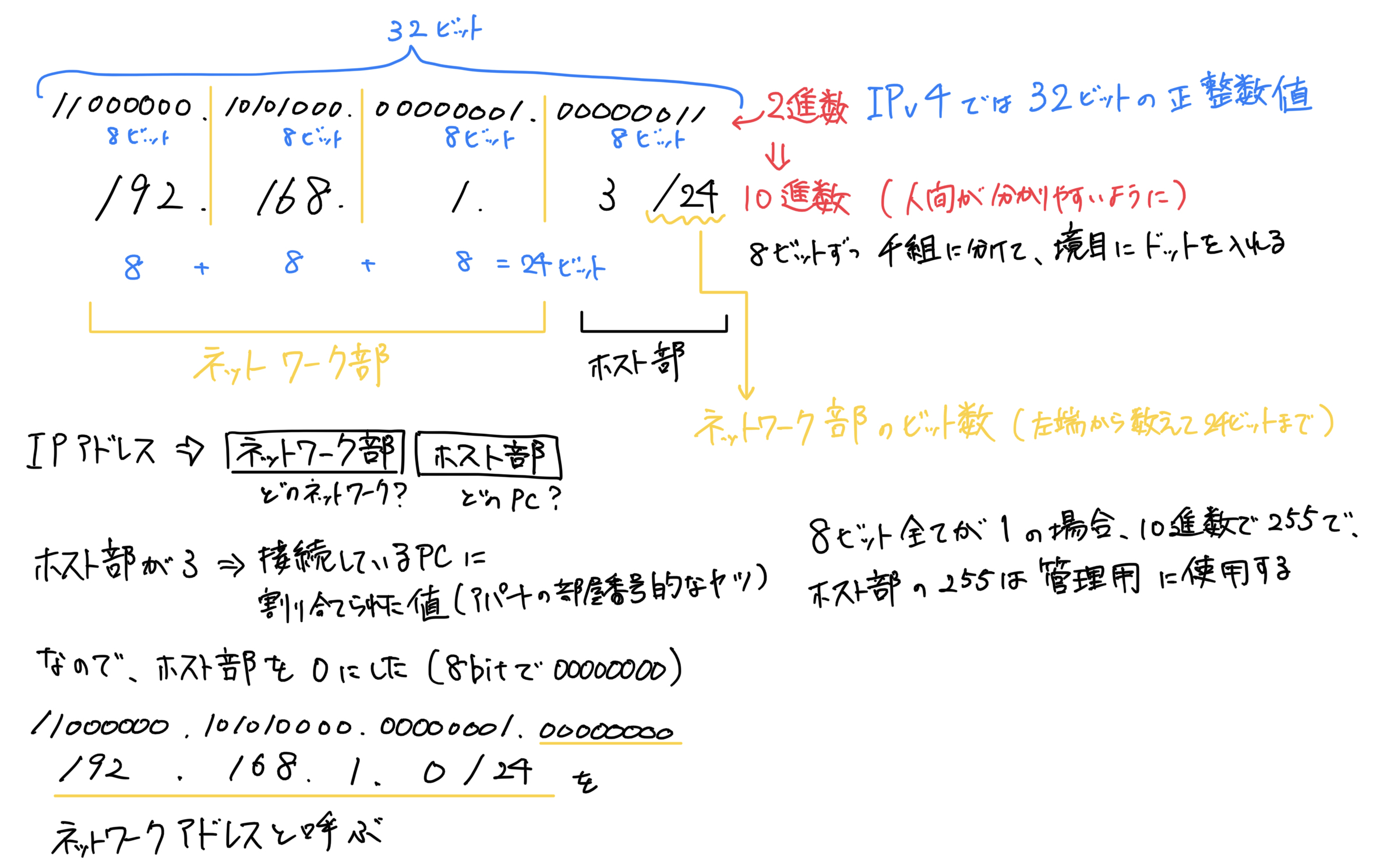
今回の問題は「IPv4」の仕組みを理解する事です。この問題を解くには、2 進数と 10 進数を相互に変換すること、8 ビットや32 ビットという用語も知っている必要があります。

「2 進数と 10 進数を相互に変換する」部分に関しては、別途解説記事を書こうと思いますので、お待ち下さい。待ちきれない方は、検索すると分かりやすい方法がすぐ出てきますので、トライしてみて下さい。

IP アドレスにはネットワーク部とホスト部があり、前者はどのネットワークに属しているか、後者はどのネットワーク機器かを表します。

基本的には「192.168.1.3」などの 10 進数をドットで区切った値からドット毎に 2 進数に変換していく事で正解出来ます。
2 進数とは 0, 1 の次に 2 になる時に、10 進数でいう 9→10 になるときのように、位が変わります。「2」→「10」と表すわけです。

• 「192」→「11000000」
• 「168」→「10101000」
• 「1」→「00000001」
• 「3」→「00000011」

以上のように変換されるため、「11000000.10101000.00000001.00000011」が 2 進数で表した IP アドレスになります。以上を踏まえて、画像をご確認ください。

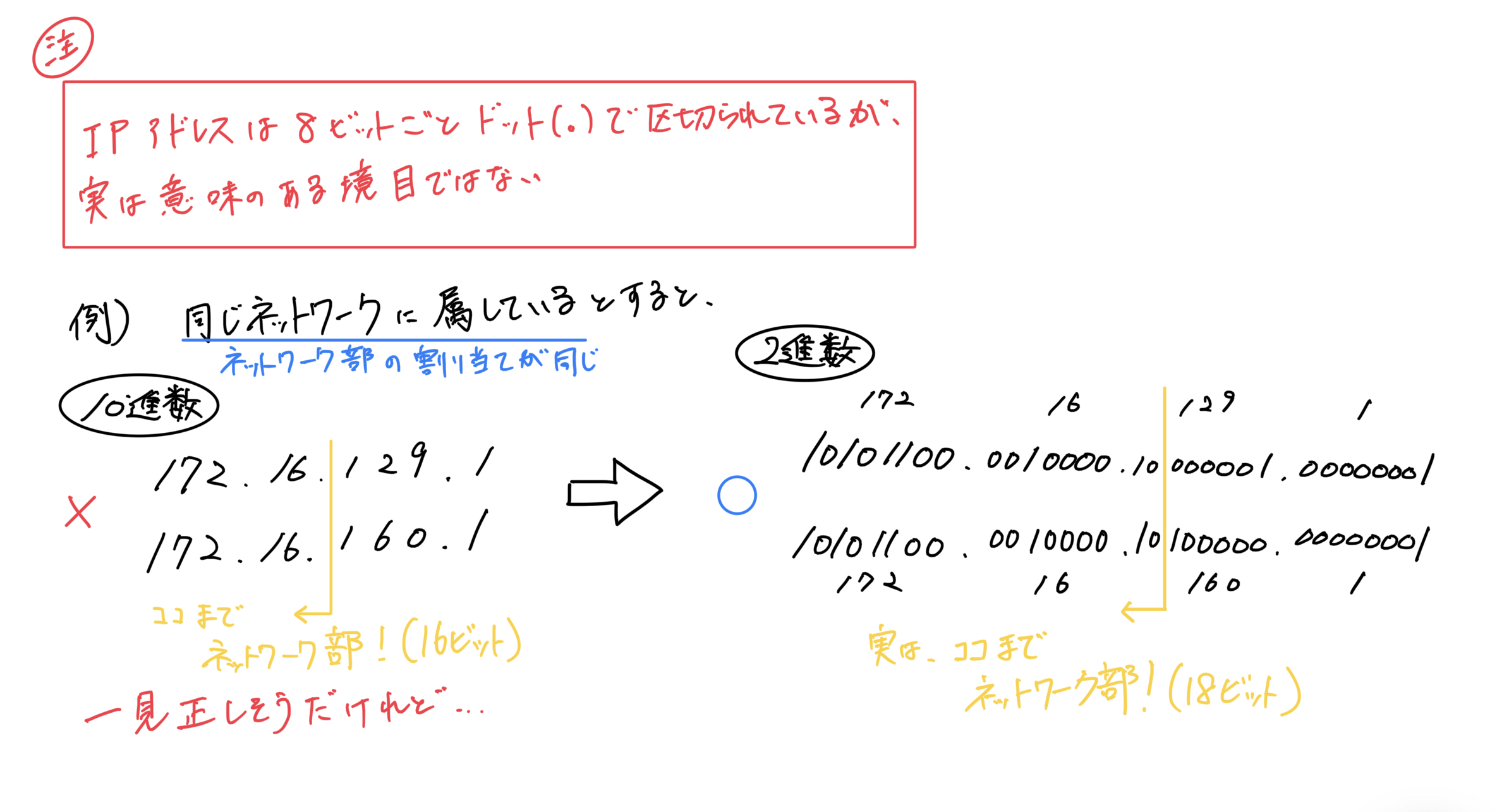
こちらは、解答セ、ソの解説です。同じネットワークに属しているという条件があるため、提示された「172.16.129.1」と「172.16.160.1」のネットワーク部は、同じはずと考えられます。すると、たとえ解答セ、ソが隠されていても、2 つの IP アドレスの 2 進数表記で、上から同じ数までを数えれば、ネットワーク部に割り当てられたビット数が分かるという仕組みです。

戻って、解答シ、スの解説です。
そもそも、8 ビット「00000000」〜「11111111」までは、10 進数でいくつまで表しているのでしょうか。実は、0〜255 までです。

0 から 255 まで表せる 8 ビットには 256 台のネットワーク機器を割り当てられるという事になります。ここで着目するべきは、K さんの発言です。「0 とすべてのビットを１にしたものが利用できない」という文言から、「0」→「00000000」、「すべてのビットが 1」→「11111111」で、256 - 2 を表しています。

詳しく言うと、0 はネットワークアドレス、255 は管理用の割り当てになるので、各ネットワーク機器には末尾の８ビット分がホスト部だとすると、(256 - 2)台分、割り当てられます。
しかし、それだと、254 コと言うことになり、65,534 台には遠く及びません。ということは、もう一つ８ビット分、ホスト部に与えられていると予想できますね。すると、(256✕256 - 2)台分は接続できるということになります。

第 2 問

比例代表選挙の当選者を決定する仕組みを図や会話を元に、擬似コードで表現する問題。
プログラミング経験の有無で大きく差が開く（主に解答速度の面で）と考えられる。かと言って論理的な思考力があれば、正解することは十分に可能な問題と思われます。

オンラインの実行環境（ブラウザ上でプログラミングを実行できる）で有名なサイトは、

>> paiza.IO

などがあります。無料で、有名なプログラミング言語を練習出来るので、試してみて下さい。

問１（１議席の重みを決めて、各得票数を割るという方式）

配列や添字といった、プログラミングに関する背景知識は必須です。普通科の「情報 I」でどのようなプログラミングをするか、きちんと確認する必要がありそうです。
また、擬似コードの作成なので、授業で扱うプログラミング言語で差はあまりない印象です。

以下では、各擬似コードを「C 言語」で組んだものになります。おそらくは、「Python」などで記述するほうが簡単です。お好みの言語で記述して、動かしてみましょう。ネット上の環境で試せるので、現在高校生の方は、実際に真似して書いてみる事をオススメします。

サンプルでは Python に近い擬似コードの書き方（条件文の後ろに:など）でしたが、=(イコール)を左の変数、配列への代入として捉える事が重要です。

問 3 の図 3 の擬似コードを C 言語で記述（なるべく擬似コードに近いコードを目指しました）

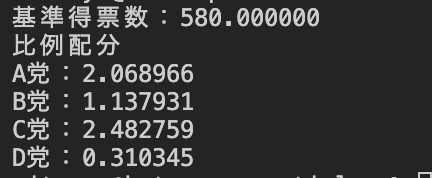
info_exam_q2_1_sample.c
#include <stdio.h>

int main(void) {

    char *Tomei[4] = {"A党","B党","C党","D党"};
    int Tokuhyo[4] = {1200, 660, 1440, 180};
    int sousuu = 0;
    int giseki = 6;

    int m;

    for (m=0; m<=3; m++) {
        sousuu = sousuu + Tokuhyo[m];
    }

    double kizyunsuu = sousuu / giseki;

    printf("基準得票数：%f\n", kizyunsuu);
    printf("比例配分\n");

    for (m=0; m<=3; m++) {
        printf("%s：%f\n", Tomei[m], Tokuhyo[m]/kizyunsuu);
    }

    return 0;
}

上記のプログラムを実行すると、コンソール画面に以下の結果が出力されます。サンプル pdf の本文にも記載されている結果になっています。

問 2 各政党の得票数を整数で割った商の大きい順に議席を配分する方法 （図８に手書きで値を書き込んでみる事が重要）

本文の話の流れで、問題点がいくつか挙げられ、それを改善した配分方法を試してみます。慣れるまでは、頭の中で手順を無理やり考えることはやめましょう。図７や図８を印刷した紙に直書きでいいので、手順を繰り返す度に、変化していく値を鉛筆で入れていきましょう。

問３ 擬似コードの書き方に慣れておこう

問２で繰り返す手順を十分に理解したところで、擬似コードにしていきます。

問 3 の図 9 の擬似コードを C 言語で記述（なるべく擬似コードに近いコードを目指しました）

前回のコードとの違いは、「各政党の得票数（Tokuhyo[maxi]）」を「その政党の当選者数+1（Tosen[maxi]+1）」で割り、その商を表２における比較する値用の配列 Hikaku[maxi]に格納するという部分。繰り返しの中で、当選者数が増えているという部分の理解が重要。

info_exam_q2_2_sample.c
#include <stdio.h>

int Kirisute(int a, int b) {
    double result = a / b; // 割り算
    int kirisute_number = result; // 切り捨て
    return kirisute_number; // 結果を返す
}

int main(void) {

    char *Tomei[4] = {"A党","B党","C党","D党"};
    int Tokuhyo[4] = {1200, 660, 1440, 180};
    int Tosen[4] = {0, 0, 0, 0};
    int tosenkei = 0;
    int giseki = 6;

    int Hikaku[4];

    int m;
    for (m=0; m<=3; m++) {
        Hikaku[m] = Tokuhyo[m];
    }

    int i, max, maxi;

    while (tosenkei < giseki) {
        max = 0;
        i = 0;
        for (i=0; i<=3; i++) {
            if (max < Hikaku[i]) {
                max = Hikaku[i];
                maxi = i;
            }
        }
        Tosen[maxi] = Tosen[maxi] + 1;
        tosenkei = tosenkei + 1;
        Hikaku[maxi] = Kirisute(Tokuhyo[maxi], (Tosen[maxi]+1)); // 割られる数と割る数を切り捨て関数に渡す
    }

    int k;
    for (k=0; k<=3; k++) {
        printf("%s：%d名\n", Tomei[k], Tosen[k]);
    }

    return 0;
}

本文の流れに沿って、候補者の人数を考慮したプログラムに変更

info_exam_q2_3_sample.c
#include <stdio.h>

int Kirisute(int a, int b) {
    double result = a / b; // 割り算
    int kirisute_number = result; // 切り捨て
    return kirisute_number; // 結果を返す
}

int main(void) {

    char *Tomei[4] = {"A党","B党","C党","D党"};
    int Tokuhyo[4] = {1200, 660, 1440, 180};
    int Tosen[4] = {0, 0, 0, 0};
    int Koho[4] = {5, 4, 2, 3}; //候補者の人数を追加（C党の候補者が足りなくなる設定）
    int tosenkei = 0;
    int giseki = 6;

    int Hikaku[4];

    int m;
    for (m=0; m<=3; m++) {
        Hikaku[m] = Tokuhyo[m];
    }

    int i, max, maxi;

    while (tosenkei < giseki) {
        max = 0;
        i = 0;
        for (i=0; i<=3; i++) {
            if (max < Hikaku[i] && Koho[i] >= (Tosen[i]+1)) {
                max = Hikaku[i];
                maxi = i;
            }
        }
        Tosen[maxi] = Tosen[maxi] + 1;
        tosenkei = tosenkei + 1;
        Hikaku[maxi] = Kirisute(Tokuhyo[maxi], (Tosen[maxi]+1)); // 割られる数と割る数を切り捨て関数に渡す
    }

    int k;
    for (k=0; k<=3; k++) {
        printf("%s：%d名\n", Tomei[k], Tosen[k]);
    }

    return 0;
}

本文の先生が述べている通り、C 党の候補者が足りなくなります。
if 文（条件文）に候補者の人数が、当選者の人数以上の場合という条件を加えた事で、C 党の値では max を更新しません。
その分、次に Hikaku 配列にある値が大きい、A 党に当選者を増やした結果が得られました。

第 3 問

問１〜問４まで答えていきます。データ処理（四分位範囲、相関関係）に関する、中学、高校数学の知識が必要です。
図１で各項目の関係を表す様々な図がありますが、面食らう事無く、一つ一つ丁寧に見ていきましょう。

問１

図１の相関係数あ〜かの数値に注目。相関係数とは 0〜1 の間で表され、1 に近づくほど相関が高いと言えます。一方が増えるともう一方も一定の割合で増えている相関を正の相関。対して、一方が増えるともう一方が一定の割合で減少する相関を負の相関といいます。相関がないということは、相関係数が 0 に近いということになります。

「予選敗退チーム」はほとんど相関がないので、相関係数は 0 に近い。「決勝進出チーム」には負の相関があるので、相関係数が 0 に近くなく、マイナスであるものを探していきます。すると、「う」の相関係数が最も近い項目となるため、縦軸、横軸のデータが解答となります。よって解答ア、イは、「得点」と「反則回数」。

同様に相関係数に着目して、「決勝進出チームと予選敗退チームには相関係数の符号が逆符号で差が最も大きい」とあることから、0.527 と-0.333 から、「え」を特定。「え」と同じ縦横軸を持ち、散布図になっているものは、D である。

解答エは ②。「全参加チームについて正の相関があり、決勝進出チームと予選敗退チームのいずれも負の相関がある」という事だが、決勝進出チームと予選敗退チームを合わせると全参加チームになるので、その場合、全参加チームには負の相関があるはずだとわかります。

問 2 計算自体は中学生でも解ける内容。（焦らずに解く計算力を測る）

解答オ、カは 16 となる。「100 本につき、」という事で$x=100$として、得点増加数を実際に計算します。得点増加数は、各関数の傾きから、決勝進出チームは$0.008\times100=0.8$、予選敗退チームは$0.0064\times100=0.64$となり、その差は、0.16 となります。

解答キは 4。先程と同様に、$x=320$として、今度は、一試合あたりの得点（y）を出すと、

• 決勝進出チーム
  • $y= 0.008 \times 320 - 1.4307 = 1.1293$
• 予選敗退チーム
  • $y = 0.0064 \times 320 - 0.9567 = 1.0913$
• 得点の差
  • $y = 1.1293 - 1.0913 = 0.0380$

よって、0.0380 の少数第三位を四捨五入すると 0.04 となります。

解答ク、ケは、56。

• ある決勝進出チームの予想得点
  • $y = 0.008 \times 384.2 - 1.4307 = 1.6429$
• 予想得点と実際の得点の差
  • $2.2 - 1.6429 = 0.5571$

よって、0.5571 の少数第三位を四捨五入した値は、0.56 となります。

問 3 　四分位範囲などのデータの分析に関する知識を問う

• 決勝進出チームの四分位範囲は、$103.50 - 92.25 = 11.25$から 11.25
• 予選敗退チームの四分位範囲は、$98.00 - 87.67 = 10.33$から 10.33

よって、予選敗退チームの方が、データの散らばりは小さいという事になります。

• 決勝進出チームの標準偏差は、0.82
• 予選敗退チームの標準偏差は、0.78

よって、決勝進出チームの方が散らばりが大きいという事になります。

したがって解答コ、サは、

• 「四分位範囲の視点で見ると、ロングパス本数のデータの散らばりは決勝進出チームよりも予選敗退チームのほうが小さい」
• 「反則回数の標準偏差を比べると、決勝進出チームの方が予選敗退チームよりも散らばりが大きい」

問 4 文章からデータを正しく読み取り、処理する能力を問う

解答シは、「図 1 の ④ のヒストグラムでは決勝進出チームの方が予選敗退チームより分布が左にずれている」

問 1 で、ヒストグラムに着目していた方は、すぐ分かるが、一試合当たりの得点は決勝進出チームが高いと予想がつく。そのため濃い色のヒストグラムが、決勝進出チームだと分かるため、④ の分布が左にずれていることも正しいといえます。

解答スは、「決勝進出チームのうち、一試合当たりの反則回数が全参加チームにおける Q3 を超えるチームの割合は約 19%」という部分から、

• $16 \times 0.19 = 3.04$

より、約 3 チームだと言える。Q3 を超える全参加チームは 7 なので、予選敗退チームで Q3 を超える数は 4 だと分かります。

解答セ、ソは、「一試合当たりの反則回数がその第一四分位数より小さいチームの中で決勝進出したチームの割合」の％表記。
Q1 未満の決勝進出チームの欄は 8-2=6 と自明であることから、決勝進出チーム（Q1 未満）÷ 　全参加チーム（Q1 未満）に当てはめると、

• $6\div8=0.75$

よって、75%が答えとなります。

まとめ

全ての問題を解き終えてみて、単純な比較はもちろん出来ないですが、数学等を共通テストで十分に得点することを基礎の完成と捉えると、
このサンプルを十分に解き切る能力は、相対的に少ない時間で完成するのでは無いかと考えます。

一点、プログラミングに関する擬似コード作成に関しては、いくつかの基礎的な演習問題を実際に手を動かしてプログラミングするのが有効かと思います。期待通りに動かなかった際に、ミスを見つけ修正する能力を磨いておくことが、本番でも焦らずに擬似コードを作り切る事に繋がります。