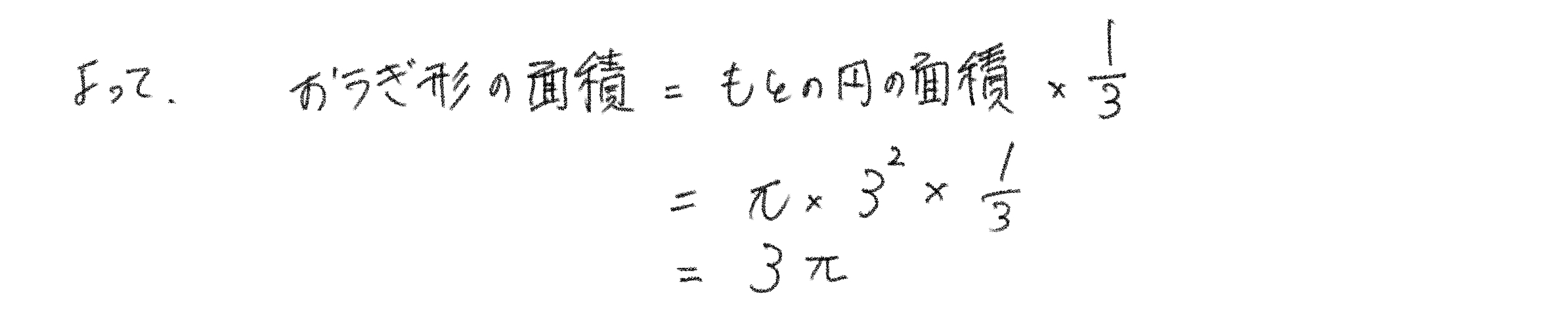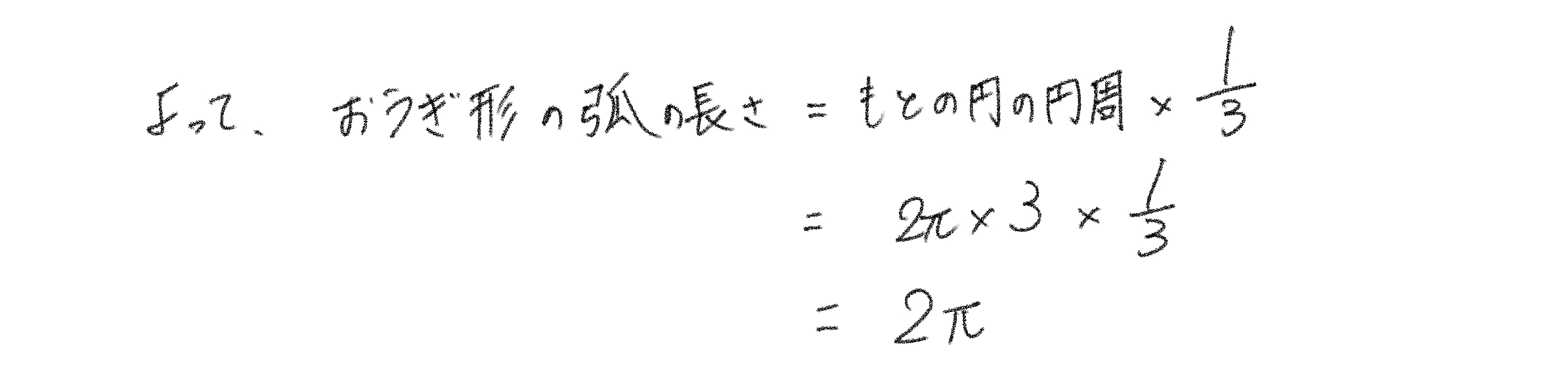求め方からおうぎ形の面積と弧の長さの公式を理解する
小須田
公式は無理して覚えないこと
多くの生徒さんが、公式が覚えられないとよく言ってきます。
私はその時、「公式は、無理して覚えない事がコツだよ」と返します。
学校の授業はよく出来ています。数学は教科書に公式が載っているけれども、決してただ載せっぱなしなわけではありません。その公式の成り立ちの解説や使い方があり、先生もそれを授業で教えてくれるはずです。
その公式の成り立ちを理解することで、いとも簡単に公式を使えるようになるはずです。
以下では、中学1年生で習うおうぎ形の公式の説明していきます。
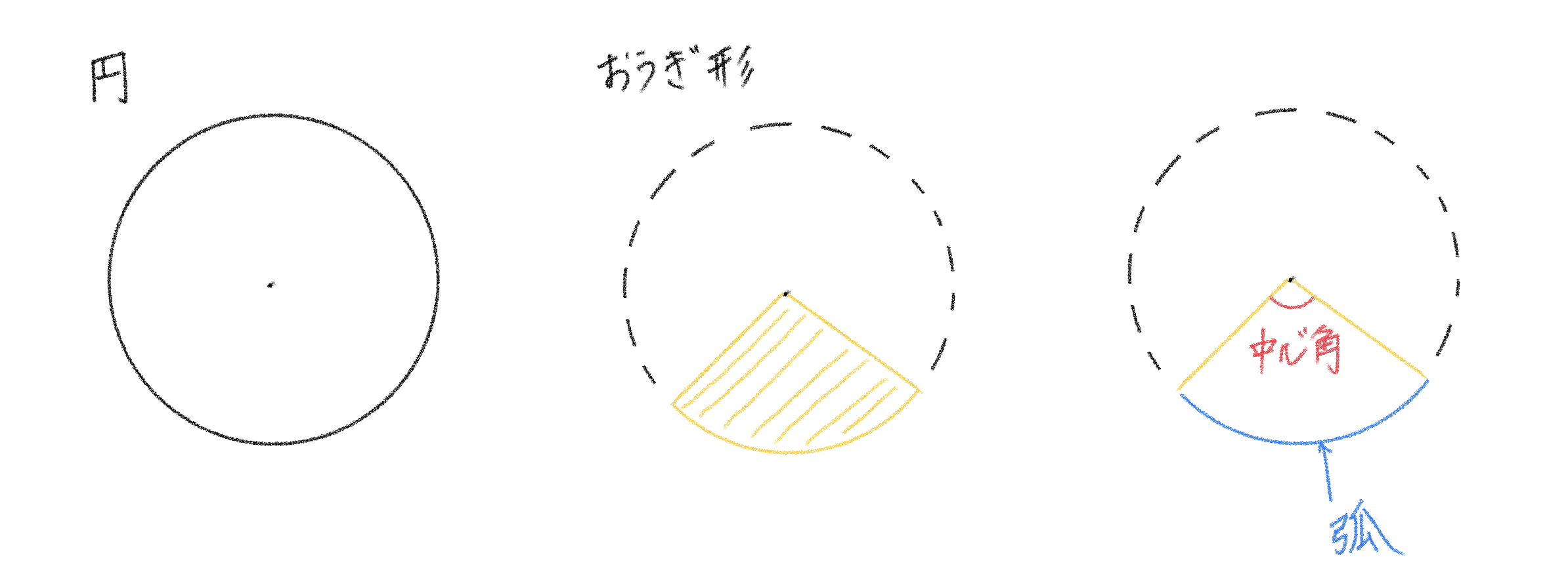
おうぎ形とは?
おうぎ形とは、2本の円の半径とその間の円弧に囲まれた図形のことです。ピザやケーキの一切れのような形ですね。
2本の円の半径によって出来る角度の事を「中心角」と呼びます。また、ピザで言う耳の部分にあたる曲線部分を「弧」と呼びます。
中学数学では、「おうぎ形の面積」と「弧の長さ」を求める問題が出てきます。中には円錐を使った表面積を求める問題でも必要になります。
そのため、おうぎ形の公式を覚える必要がありますが、丸暗記しろというわけではありません。
なぜ「そのような公式になるのか?」の仕組みを理解することで、自分で公式を導けるようになります。
おうぎ形の面積の求め方
おうぎ形はそもそも、大きな円の一部分なので、
- おうぎ形のもとになる円の面積を考えます。
- 求めた円の面積のうち、おうぎ形の部分が占める割合を求める。
この手順で、以下の例題を解いていきます。
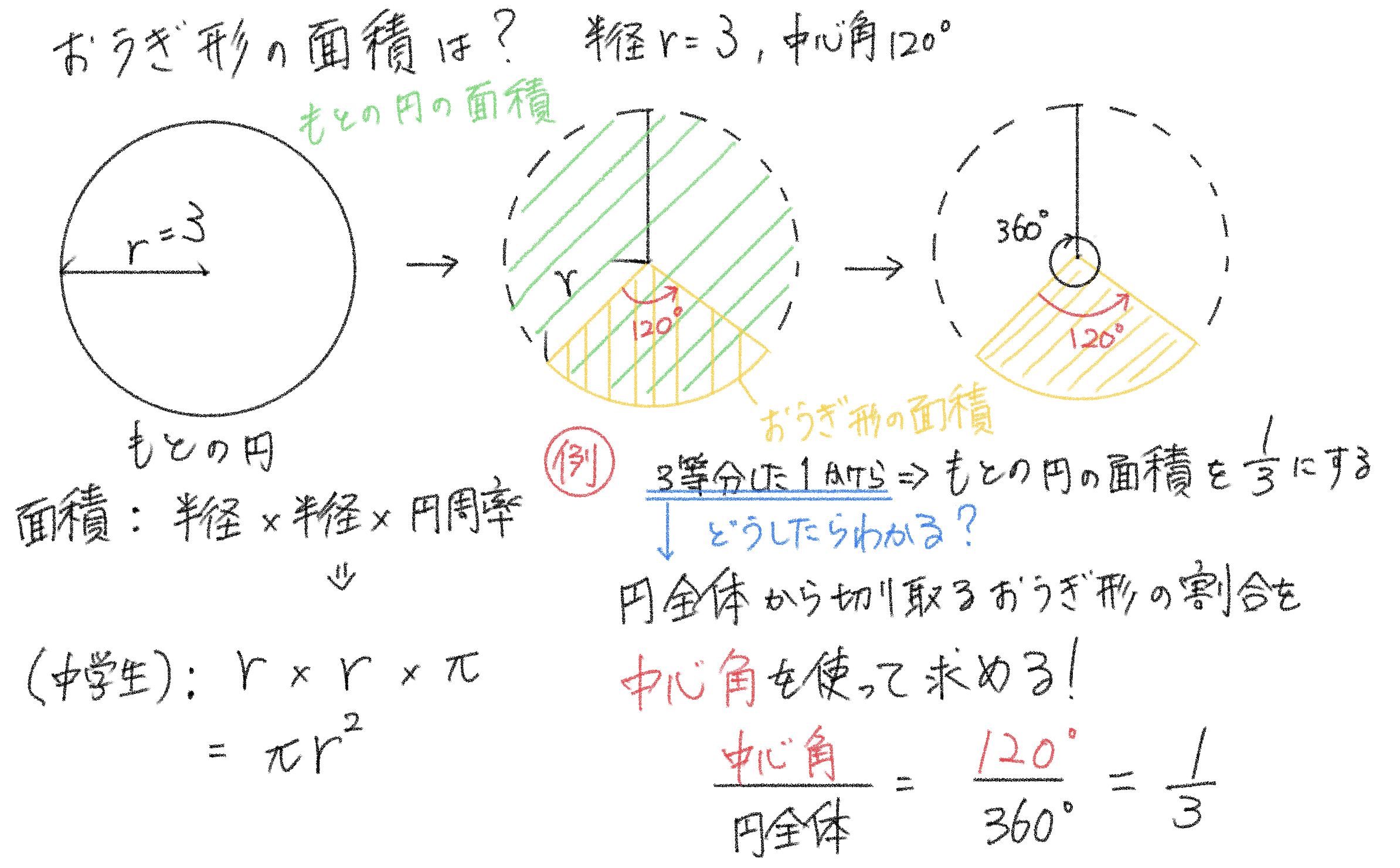
例題: 半径3cm、中心角が120°のおうぎ形の面積を求めなさい。
① おうぎ形のもとになる円の面積
半径3cmなので、円の面積の公式から、(ここは割愛します)
ですね。
② もとの円の面積のうち、おうぎ形の部分が占める割合を求める
ここさえ理解できれば、自由自在に公式を導くことができます。
以下の画像にあるとおり、図で見ると、円を3等分しているように見えますね。すると直感的に元の円の面積をにしてあげればいいと分かります。
ですが、「3等分すればいい」とどうやって導くのでしょうか。
そこで必要になるのが、「中心角」です。
中心角が大きくなれば、おうぎ形そのものも大きくなるように、中心角の大きさとおうぎ形の面積は対応していることがわかります。
とすると、もとの円の面積に対して、おうぎ形の面積を比較するために、「中心角」で比較すれば、同様の割合になると考えられますね。
よって、
実際の計算は以下の画像の通りです。
おうぎ形の弧の長さの求め方
面積の出し方が分かってしまえば、後は簡単です。
というのも、弧の長さの出し方は、面積と同様に比例式から求められるからです。
面積と同様の手順で、以下の例題を解いていきます。
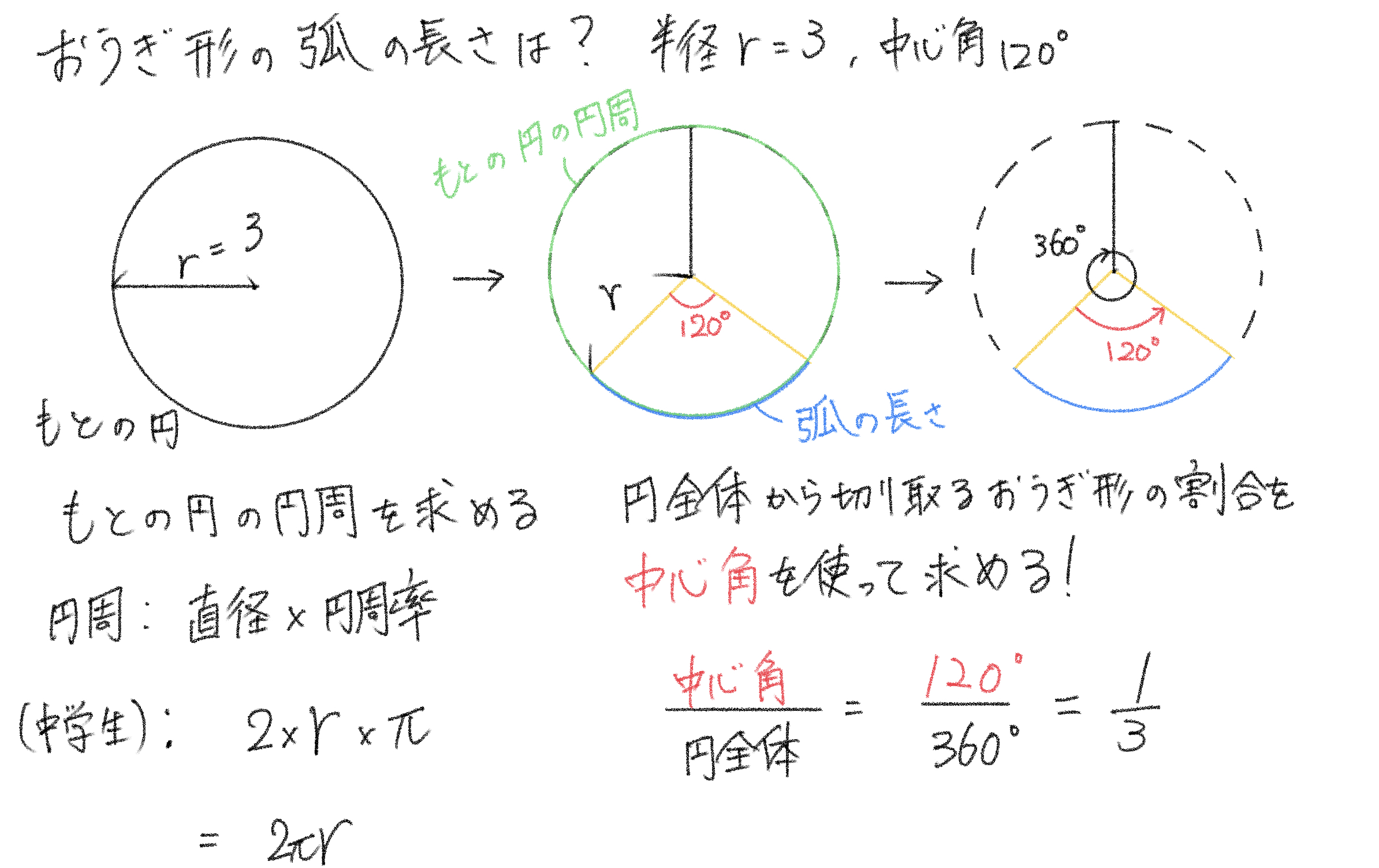
例題: 半径3cm、中心角が120°のおうぎ形の弧の長さを求めなさい。
比較するものが中心角であることに代わりはありません。
今回求めるモノは、面積ではなく弧の長さですから、円全体の弧の長さというのは、円周に当たります。
という訳で、以下のように比例式をたてることが出来ます。
よって、
このように、考え方から比例式を作ることで、おうぎ形の面積と弧の長さを出す公式まで辿り着いてしまいます。
ですから、公式をそのまま丸暗記して問題を解くのではなく、文章から比例式を立てて演習してみてください。
すると、テストの本番でも暗記した公式が出てこないという心配はなくなります。
すぐに頭の中で解法が浮かぶため、その場で比例式を組み立てられるはずです。
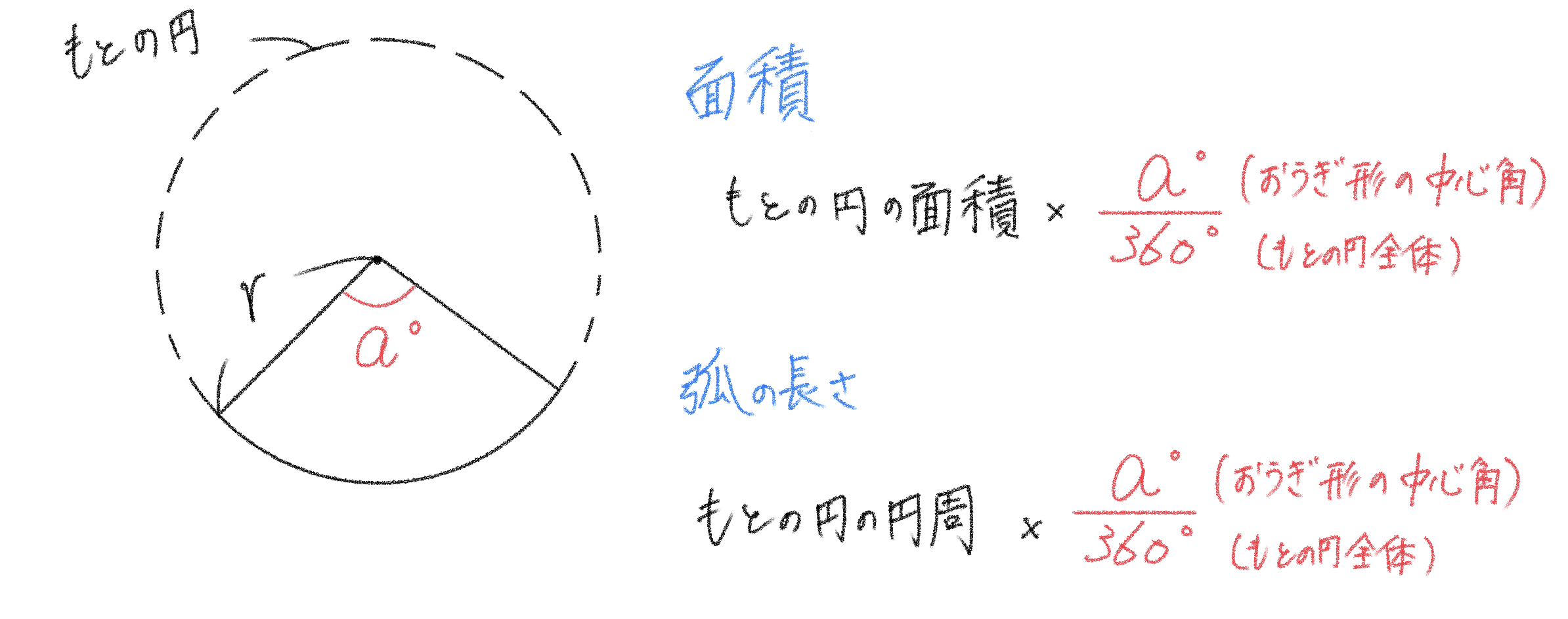
おうぎ形の公式
中学3年生は、一学期の中間テストでおそらく一年生の内容がテスト範囲になっていると思います。
これを機に図形の総復習をしておきましょう。
当会では、本記事のような内容をより分かりやすく授業で扱っております。
追記:今年(2022/05)の受講生の中学では、3年の一学期中間テストでバッチリこの問題が出たようです。復習しておいて良かったです。