距離、速さ、時間の文章問題の解き方を丁寧に解説
小須田
距離、速さ、時間の文章題を丁寧に解説
今回は、中学数学のつまずきがちな文章題の解き方を丁寧に解説します。
1次方程式を利用して解く問題には、パターンが存在します。
新研究などの参考書に収録される例題をきちんと理解し、同じ問題を反復することで入試問題でも十分満点を狙えます。
しかし、参考書の解説では、突然式が出来上がっていて、理解できないという方もいると思います。
文章から式を組み立てる部分に焦点を当ててみました。
文章題では図を描くこと
数学が苦手な人の多くは図を描かない人が多いです。面倒くさいという気持ちは分かりますが、その事実を認めて、改善していきましょう。
図を描くことは決して時間のロスにはなりません。むしろ、理解の助けになり、ミスを防ぎます。
疎かにしている人は、これを機に図を描いてみましょう。
それでは、例題です。
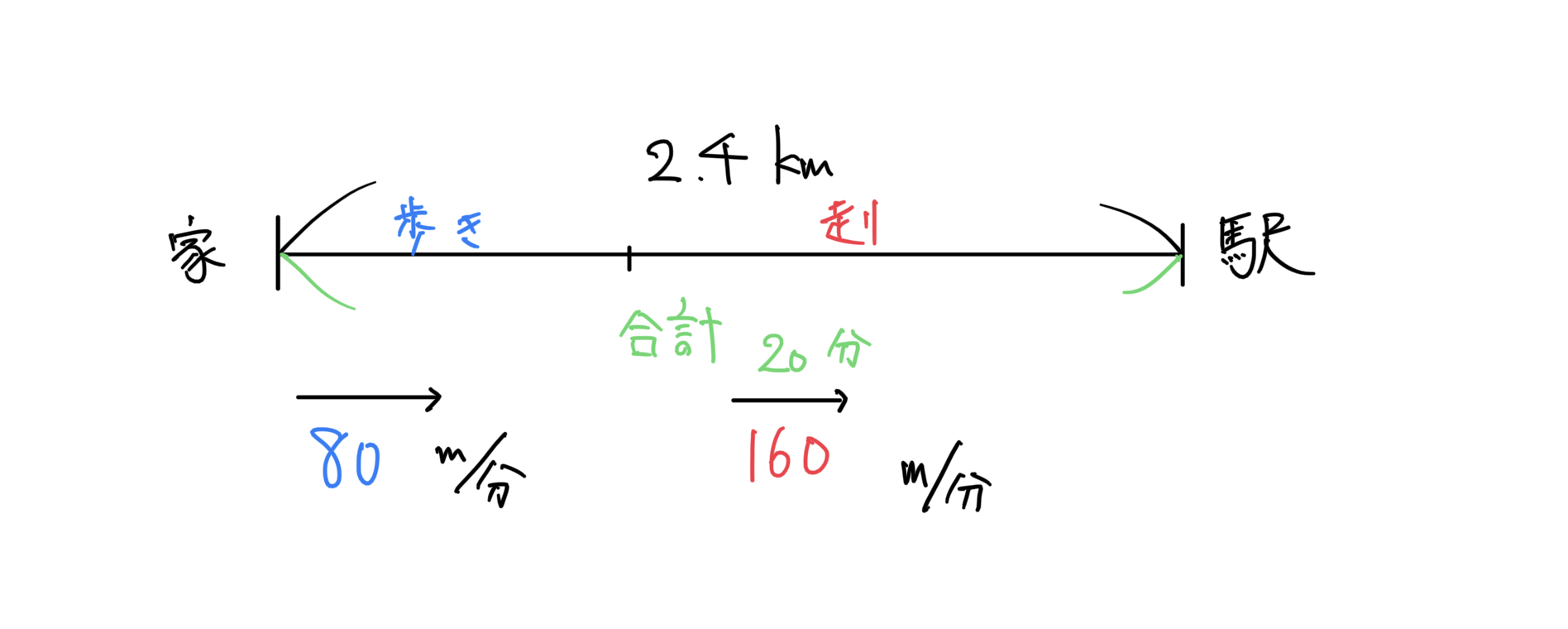
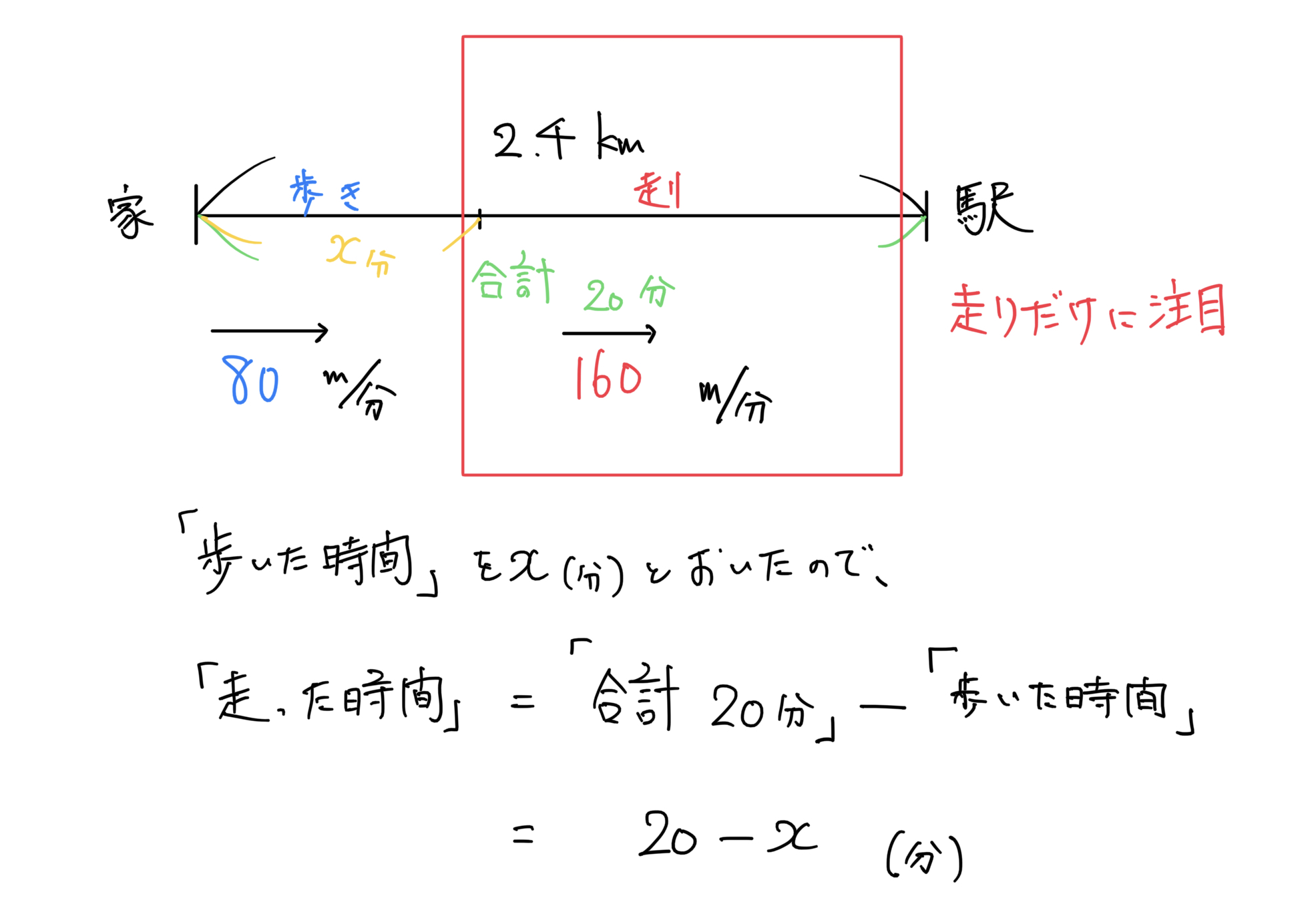
例題: 太郎さんは自宅から2.4km先にある駅へ行くのに、はじめは毎分80mの速さで歩き、途中から毎分160mの速さで走ったところ、20分かかった。このとき、歩いた時間と走った時間はそれぞれ何分間か求めなさい。
この例題から、まずは図を考えてみましょう。
文章の中で、説明されている値を入れてみた図が以下のようになります。
図の描き方
- 直線は基本的に距離を表すため、長めに描いておきます。その後、カッコを付けて2.4kmと入れます。
- 例題から直線を、「歩いた距離」と「走った距離」に分ける必要があることが分かります。
- 「歩き」側に80m/分と速さを記入
- 「走り」側に160m/分と速さを記入
- 最後に分かっている事は合計で20分だったという事を直線の下側に記入しておきます。
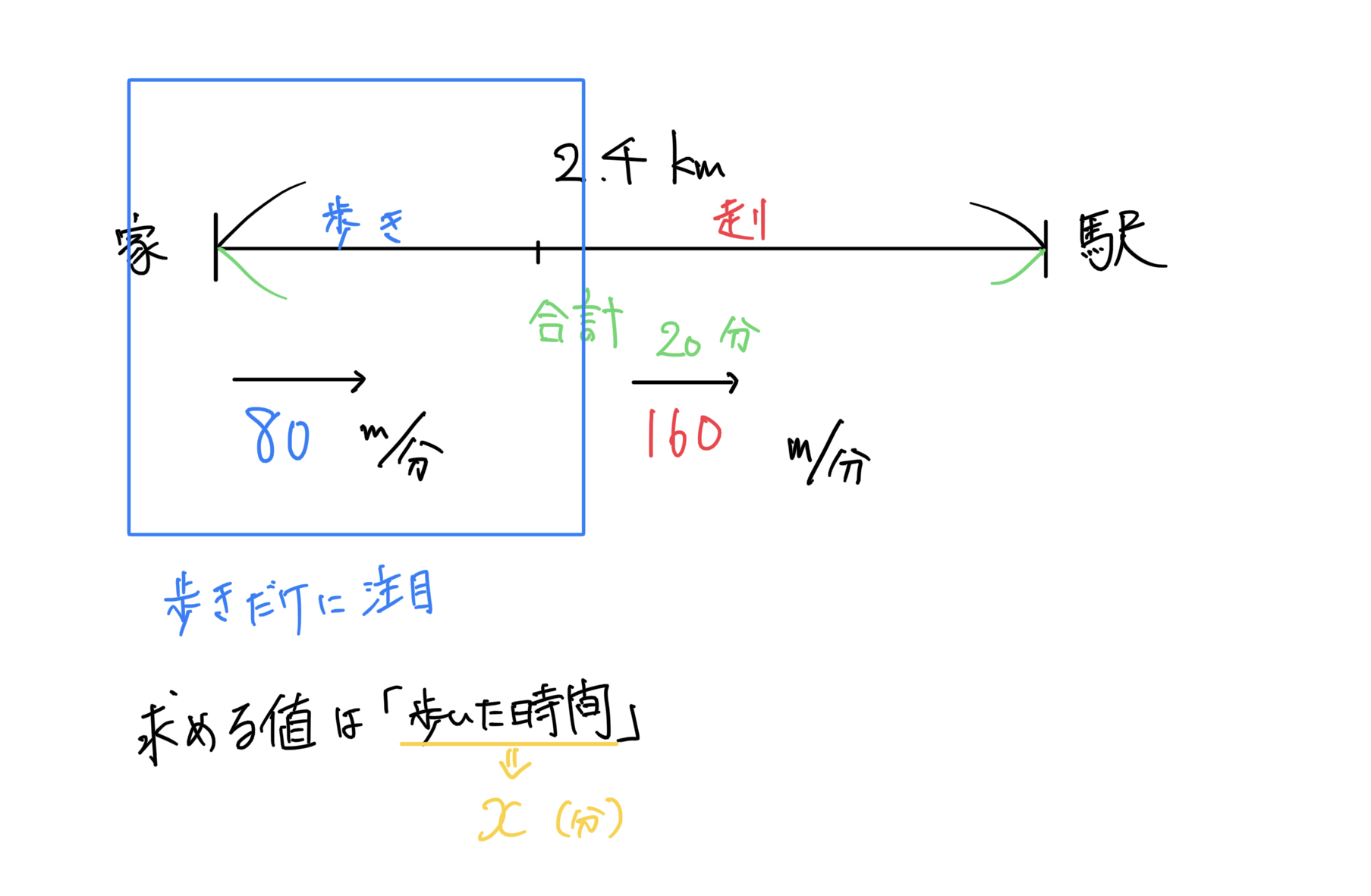
図が描けたら求めたい値を考える
先程の手順どおりに図が描けたら、文章題では何を聞かれているのか考えましょう。
問題の多くは、文の最後に「〜を求めなさい。」とあるはずです。
今回は、「歩いた時間」と「走った時間」がそれぞれ何分間か求める問題ですね。
求めたい値がある場合、その代わりに文字をおいて、計算するんでしたね。
2つの文字が必要そうに見えますが、手始めに、
とおいてみましょう。
そして、距離の問題で頭の中を整理するコツは、「速さ」ごとに分けて考えることです。
今回で言えば、「歩き」と「走り」を別々に注目してみるということです。
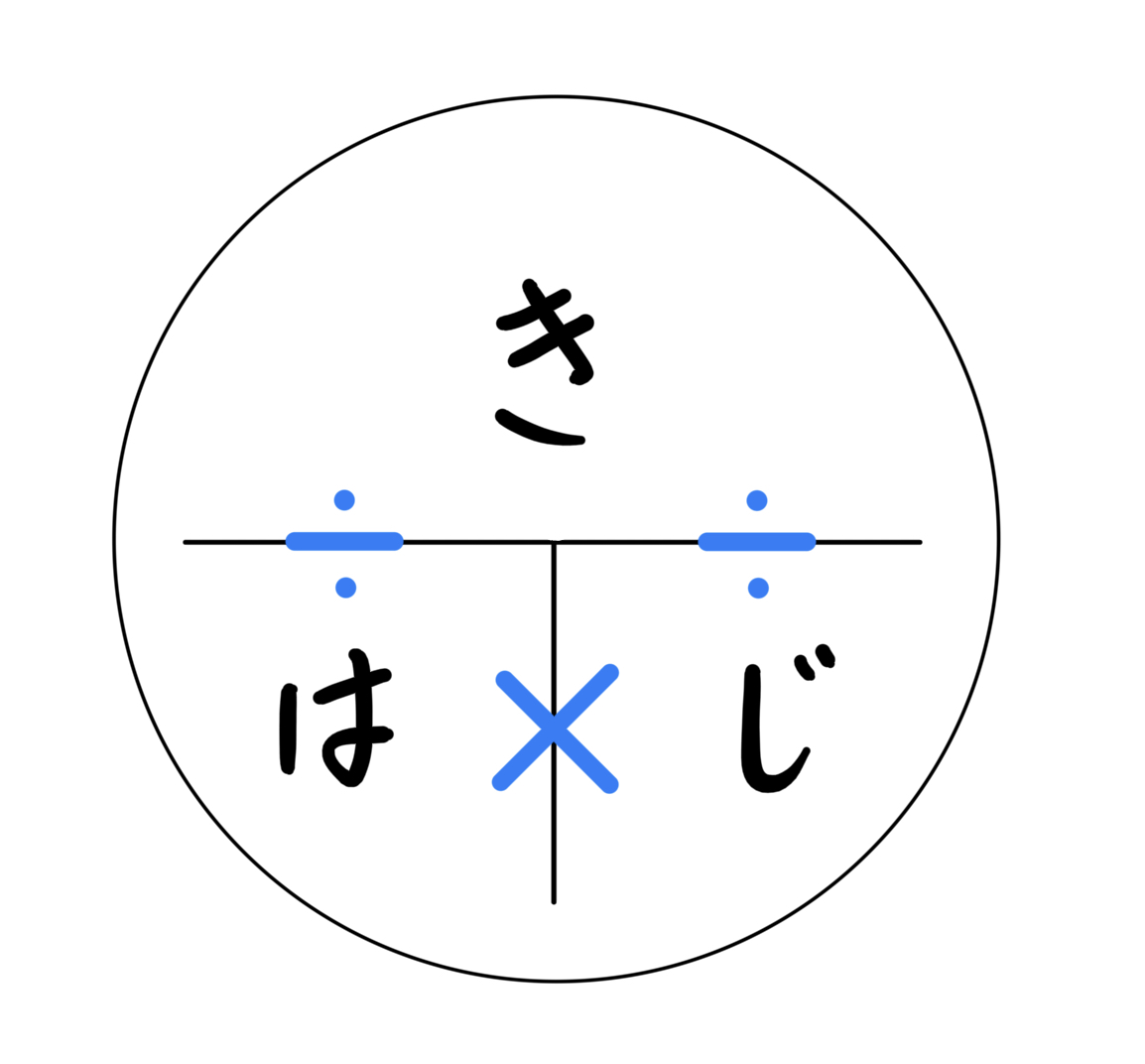
距離、速さ、時間の問題に必須の「きはじ」
「歩きの時間」を文字でおいてあげたところで、「歩き」に注目してみましょう。
図から利用できる値は、
です。ここでもう一つのポイントですが、「きはじ(みはじ、はじき、等とも言う)の法則(公式)」を理解することです。
上の図は、以下の3つの公式を、簡単に図にまとめたモノです。
図にある位置関係を覚えるだけで、公式をその場で作れるようになります。
割り算の部分は、位置関係通り、分数として理解してあげても良いと思います。
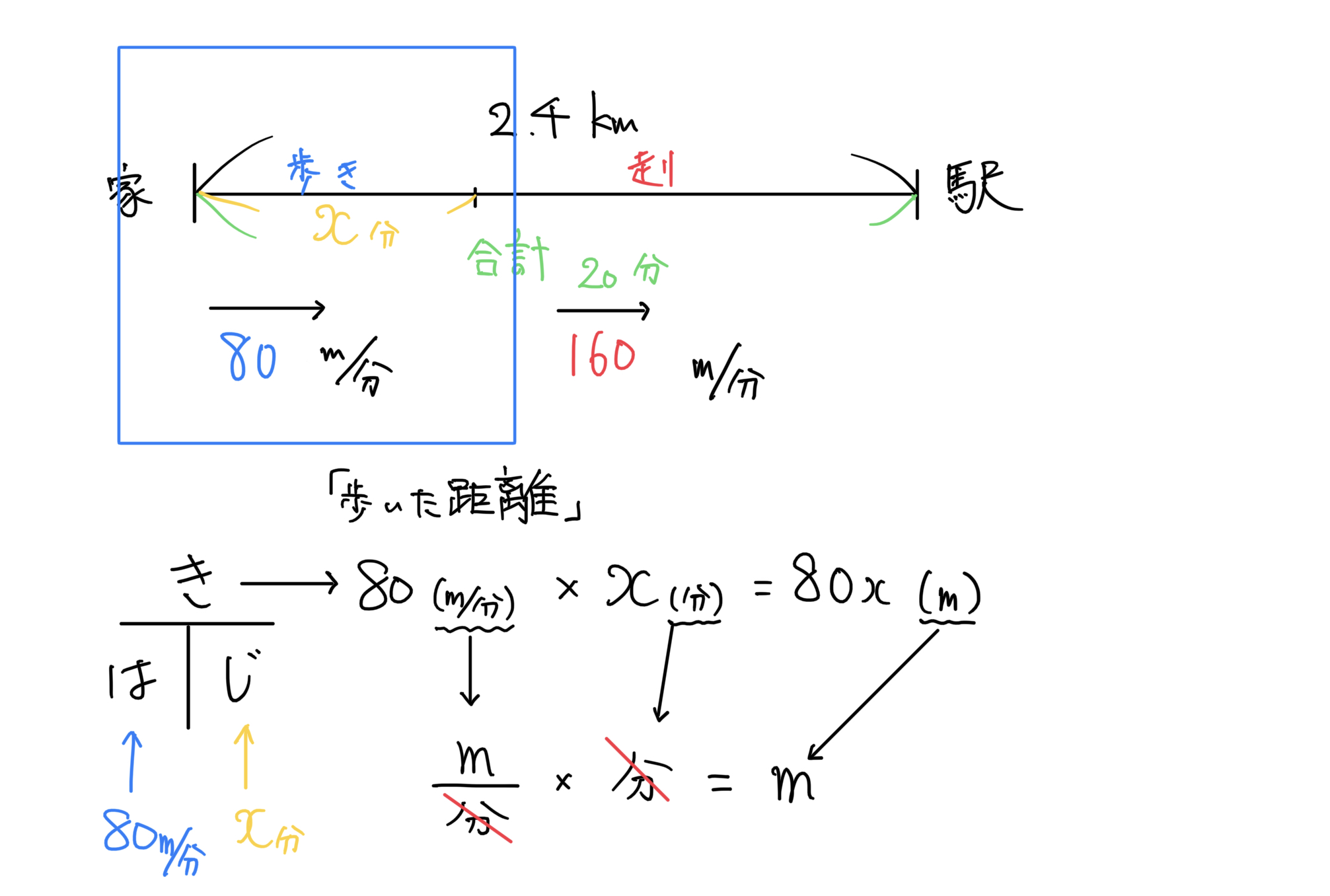
「歩き」に対して「きはじ」を使い、「距離」をあらわす
以下の図の通り、
「きはじ」を使ったときに、「速さ」に80m/分、「時間」にを入れると、足りなかった「距離」を埋めることが出来ます。
となります。
余談です(単位計算の解説)
また、図にある通り、単位に注目してみましょう。
中学生では、まだ考えた事がないかもしれませんが、単位同士を計算しても実は筋が通っているんです。
「歩いた距離」の単位はm(メートル)なので、右辺の単位を計算すると
「走り」に対して「きはじ」を使う
「歩き」と同様に、今度は「走り」に注目して、「きはじ」を使いましょう。
現状、図から利用できる値は、
だけです。
ですが先程、
とおいた事を思い出しましょう。
すると、
と、表せる事に気付きます。
あとは、以下の図の通り、
「きはじ」に「速さ」160m/分、「時間」にを入れると、足りなかった「距離」を埋めることが出来るので、
となります。
完成した図から方程式を考える
ここまでで必要な値は全て作ることが出来ました。
きちんと、自分で描いた図に書き込んでおきましょう。
すると、以下のように、
という関係に気づくことが出来るはずです。
後は、立てられた方程式を解き、を求めます。
距離の単位は全てに揃えないと計算できません。をにするため、
を忘れずに!
以下、計算式になります。
よって、歩いた時間は10分となり、
分に代入して、
で、走った時間も10分と分かります。
当会では、本記事のような内容をより分かりやすく授業で扱っております。
長野県の高校入試を見据えて、小中学生を英数メインで指導しております。(高校生も英検準一級まで、および数学と物理を指導します)
ご興味がある方は、お問い合わせ下さい。