【数値積分】台形公式をC言語で扱う

計算をC言語で記述して結果を出力する課題

現在、受け持っている生徒さん（大学生）のプログラミング課題について、面白かったので記事にしておきます。
私は、以下のような内容で生徒さんに説明しながら、プログラムを完成までお手伝いさせていただきました。

今回は、以下の問題を解くために、数値積分についての理解を深め、C言語のプログラムに落とし込む事が目的です。

数値積分とは？

（手書き）ある与えられた関数f(x), 区間[a, b]

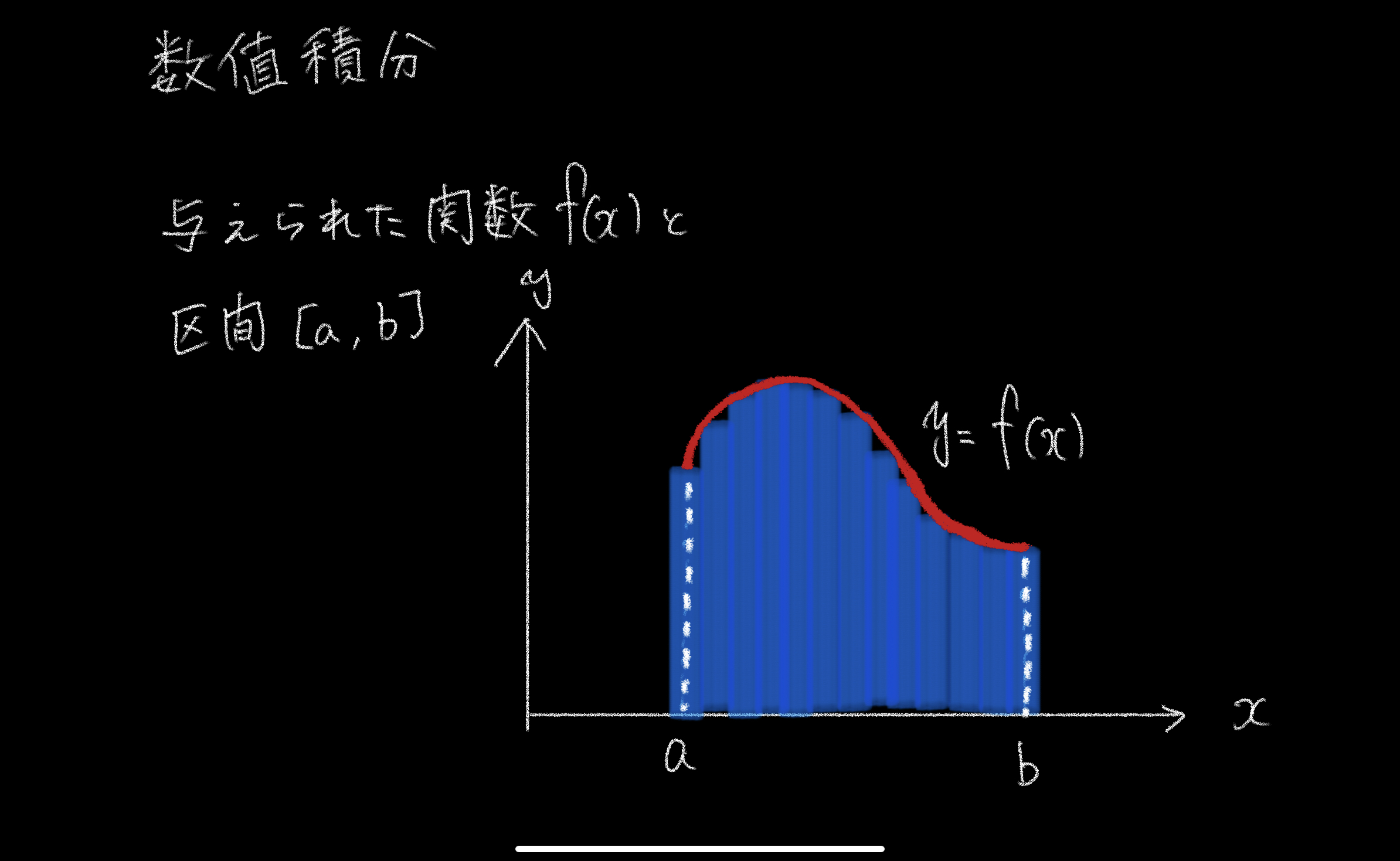
上記のように、与えられた関数f(x)と区間[a, b]があるとする。
これに対して、定積分

を「数値的」に求めることです。

基本的な考え方

基本の原理

1. f(x)をサンプリングし、各点を$\left( x_{i},y_{i}\right)$とする
2. サンプル点を通る簡単な関数 $p\left( x\right)$で$f\left( x\right)$を近似する
3. $\int_{a}^{b}f\left( x\right) dx \simeq \int_{a}^{b}p\left( x\right) dx$となり、右辺を計算する

今までの積分と台形公式について

積分を習ったときのことを思い出しましょう。

積分とは、「長方形」の帯の面積を足し合わせた総面積を求めることでした。
そして、その長方形の底辺にあたるh（幅）を小さくしていくことで近似しましたね。

では、あくまで関数f(x)が曲線だと仮定します。長方形近似だと、長方形とf(x)が交わった「角」が余分だったり、欠けてしまったりと、精度がイマイチです。

解決策として、曲線を作るある点と点を結ぶ1次関数を考えます。「長方形」ではなく、「台形」で考えてみるとどうでしょうか。はみ出ていた部分がかなり減ると思いませんか？

というわけで、長方形の代わりに台形の面積を足し合わせていく、この方法がその名の通り「台形公式」です。

台形公式を用いた数値積分のプログラミング（C言語）

台形公式の仕組み

まずは、台形公式を理解しよう。

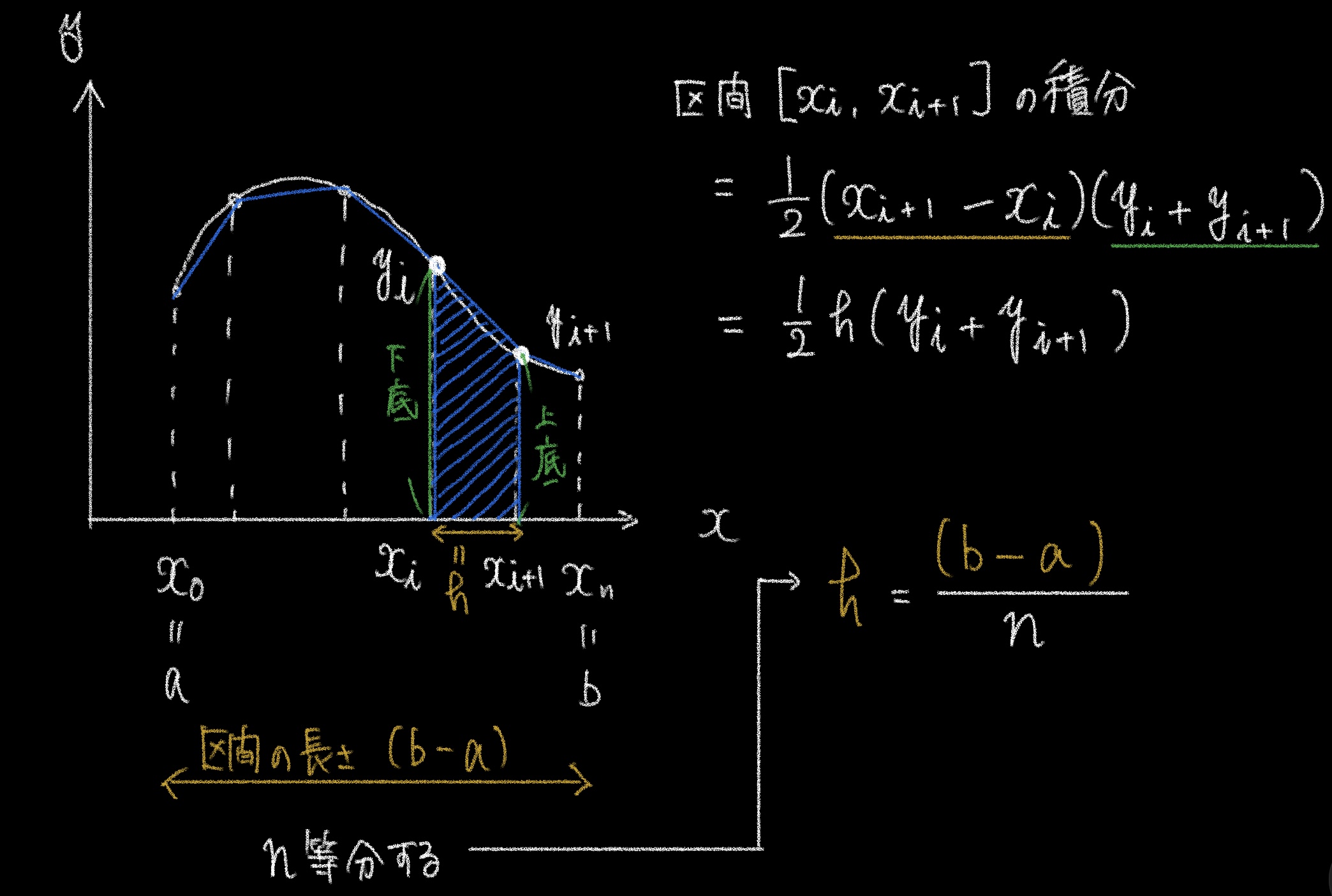
関数を1次補間で近似して積分を行う。区間[a, b]をn等分する。

区間$\left[ x_{i},x_{i+1}\right]$の積分は、

台形公式の近似の解説1

台形公式の近似の解説2

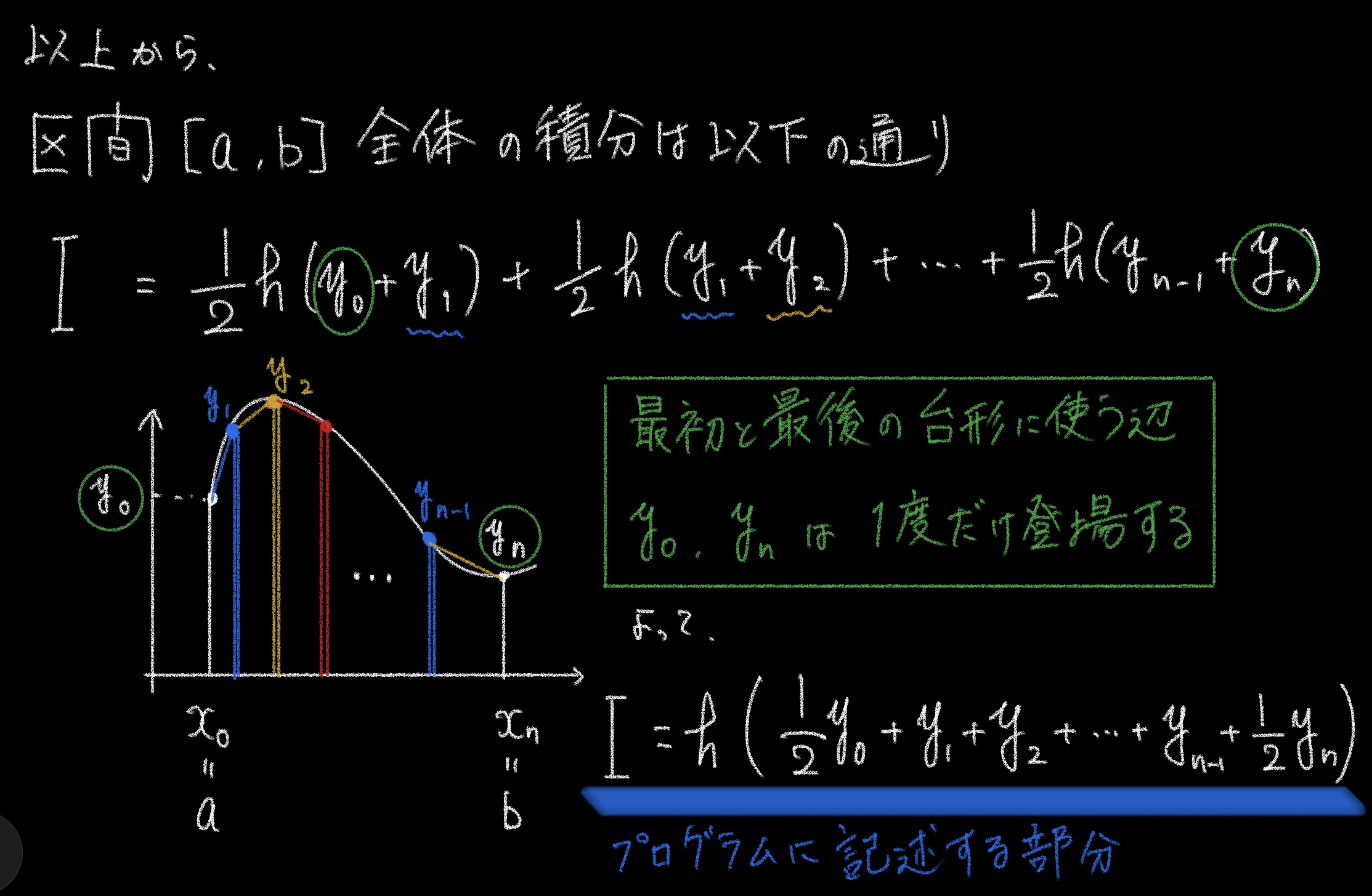
上記の計算過程を経て、区間[a, b]全体の積分は以下の式となる。

台形公式をC言語で扱う

前章で出した式

をプログラムに計算させる場合、あくまで細かく役割を分担すると分かりやすいです。

＊あくまでプログラムにした際に直感的に理解できる方法で記述しています。効率を考える場合は、別の記述方法を模索しましょう。

役割分担した計算の記述方法

1. $y_{1}$から$y_{n-1}$までの総和を計算
2. ①の計算結果に $\dfrac{1}{2}y_{0}$と$\dfrac{1}{2}y_{n}$を足す
3. ②の結果にhを掛ければ、全ての計算が終了する。

sample.c
#include <stdio.h>;

/* 被積分関数 */
double f(double x)
{ // 計算結果がπになる式
    return 4 / (1 + x * x); /* 関数f(x)の値を計算して返す */
}

double integ(double a, double b, int n)
{
    // 関数f(x)の区間[a,b]における積分を、分割数nの台形公式で解き、その値を返す
    
    double h;
    h = (b - a) / n;

    double x, sum;
    int i;

    sum = 0;

    // 1/2 * y0　を足す → y0 = a
    sum = 1/2 * f(a);

    // y1 ~ yn-1までの総和
    for (i = 1; i &lt; n; i++)
    {
        x = a + h * i;
        sum += f(x);
    }
    // 1/2 * yn を足す → yn = b

    sum = sum + 1/2 * f(b);
    return h * sum;
}

int main(void)
{
    double a, b;
    int n;

    //分割数
    n = 2000;

    // 区間[0, 1]
    a = 0;
    b = 1;

    printf("%d %10.7f\n", n, integ(a, b, n));
    return 0;
}

上記のプログラムを実行した結果

プログラム内の分割数にあたる変数を変更することで、結果が異なります。
（どれだけ、細かく台形を分割するのか決めている変数です。）

分割数(n)	計算結果(πに近いほど精度が高い)
100	3.1115760
200	3.1265885
500	3.1355920
1000	3.1385925
2000	3.1400926
計算結果がπになる式を利用した分割数と精度